
By David Innes
EDITION #5 – “What does learning look like, sound like and feel like?”
Published – 29th May 2019

David Innes is currently a Learning Specialist at Box Hill High School. He has taught for ten years in Mathematics, Science and Chemistry. He has delivered professional development sessions for the Teacher Learning Network. David has performed for the Melbourne International Comedy Festival for many years and has run an improvisational theatre troupe. David is passionate about finding new and better ways to explain concepts and to encourage students to have a better experience with mathematics.
I am obsessed with timing and structure. I get up at the same time each morning. I know that if I do not get out of bed within three minutes, I risk derailing my entire morning schedule and will miss my train. So, I promptly proceed with the following: have my shower, make my coffee, get dressed, then make my toast (Vegemite, always). By this stage, the coffee has cooled to precisely the right temperature for efficient consumption. It then takes me exactly 16 minutes, or 1,372 steps, from my front door to the station platform on foot. Can you tell I am a Maths teacher yet?
Lesson structure
I firmly believe in structure because it means the amount of stress in trying to create a product is minimised. Students love a certain amount of structure. Being a teenager is often frustrating, terrifying or confusing. After all, there are friendship groups, gossip, social media and television all telling them different things. As a teacher, we do not need to add to that stress by having what goes on in our lessons all higgledy-piggledy or our assessments difficult to understand. Developing a ‘shortest path’ to success involves teachers providing the quickest and most efficient means for a student to master a new concept (Lemov, 2010). If we can develop our explicit teaching efficiently, this can lead to more time for assessment. I had developed a very particular structure for my lessons and, in my opinion at that time, they worked. It wasn’t until I moved schools and began working with a new group of students who had no idea who I was, that I discovered parts of my lesson structure did not work.
In my lesson structure, I write a learning intention on the board which summarises, in a sentence, what I intend to cover in that lesson. I write the lesson procedure underneath. The lesson procedure is a list of dot points outlining what will happen in the lesson. I saw this when I was on teaching rounds many years ago and I think being explicit about the parts of the lesson is an effective signpost for students so they can see what we are intending to do in the lesson. My lesson procedure used to be: Warm Up, Notes, Examples, and Questions (time permitting).
(Recommended reading for learning intentions and success criteria: Clarity by Lyn D. Sharratt (Sharratt, 2018))
I would start with a warm-up activity at the beginning of class, to get students engaged and focused, then I would explicitly teach for as long as I felt was necessary to cover what we needed by a unit timeline. With some classes, I would monitor how well the students performed on the warm up activity. Most of the time I would only assess in summative fashion.
Upon arrival at my new school, it was clear this was outdated and needed to change. The students that I was teaching were already in the mindset of mathematics by the time they arrived and so a warm-up activity was just disrupting their flow of learning. They wanted to be told things, then get on with it. This forced me to re-think not just the purpose of the warm-up activity but also how I was collecting information about the students.
It was also at this point that I discovered a colleague’s brilliant mathematics teaching practice which has been dubbed the ‘Sorenson Ratio’.
The beginning of the ‘Sorenson Ratio’
I was in a meeting with fellow mathematics teachers and we were sharing our teaching practices. My colleague, Helen Sorenson, shared her approach, which I will now refer to refer to as ‘The Sorenson Ratio’. It is expressed thus:
The amount of maths the teacher is doing
<
The amount of maths students are doing
My problem in the way I was structuring lessons was that I would never give enough time for students to practise. My belief was that I should always do as many examples on the board or overhead projector as humanly possible, such that I could count every iteration of a problem a student had before they encountered such an example in their textbook. By the time I finished, students would barely have any time to work on mastering their own skill before going home and forgetting everything I said.
A new approach and a new lesson structure
I changed my structure in class. I started my lessons getting straight into the new concept, perhaps with a minimal recap of the previous class. Then I set the timer on my phone for precisely 15 minutes, with an announcement to the students that the time has started. This gave a frame to students – they knew I was only going to talk for that length of time and needed to work through as many examples as possible in that time without interruption.
The 15 minutes on the stopwatch is about the attention span for a student to listen to a teacher. For my junior students, I take ten to 15 minutes. For my senior students, 15 to 20 minutes. I only go to 20 with my senior students if it is a new concept that requires lengthy procedures (for example, learning graph transformations in Mathematical Methods). To support this, I had to make sure the examples and concepts I used were quick enough to cover mastery of all they might encounter in their practice problems. I also uploaded the notes online prior to the lesson, with additional examples, so students could download anything they missed due to absence, or the parts where I could have been ‘too fast’. By getting the explicit teaching part finished in a shorter amount of time, I could attend to students who needed more assistance on a one-to-one basis.
At my current school, the lessons are 50 minutes long – in my opinion, the perfect length. I occasionally have a double period which can be a strain on mathematics teaching and focus for students. My optimal ‘Sorenson Ratio’ is 3:7 – for every three minutes of teacher talking time, there should be seven minutes of students working time. So for a double period, no more than half an hour. The amount of time does not need to be all at once. In double periods, I try to keep my talking to a minimum. For example: ten minutes in each period, five minutes for an activity and five minutes to wrap up at the end. This is of course, what works for me and may not work for other classes. I would not recommend using this as a strict guideline. However, I would emphasise that talking less and letting students work more is important.
So how does this lesson structure enable effective formative assessment?
Formative assessment – exit tickets
After abandoning the warm-up activity, I instead implemented Exit Tickets (Lemov, 2010) for formative assessment.
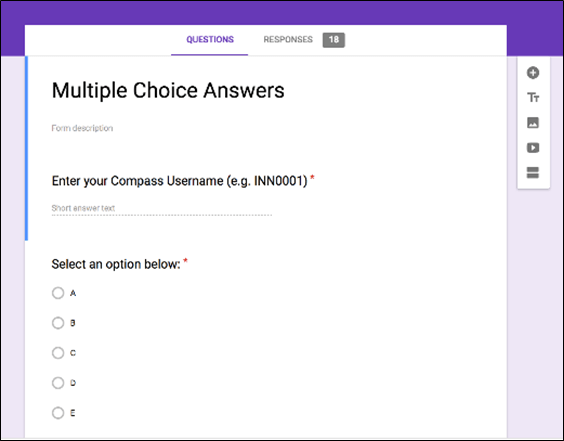
Exit tickets are a type of formative assessments where the teacher sets students a task to complete in the last five or ten minutes of a lesson to see what they have retained from the beginning. This can be done in a multitude of ways, but like all teachers I am keen to minimise my workload and collecting piles of paper. I developed an online resource to complete the data collation efficiently and effectively.
At the end of a lesson, I project a multiple-choice question on the screen (for example, a Victorian Curriculum Assessment Authority Exam Question), with a link to a Google Form. Students enter their results and their student code. I only reveal the answer when I have had all students submit, a ‘No Opt-Out’ strategy (Lemov, 2010). Once all students have entered their answers, I reveal the statistics for the class (how many students chose A, chose B etc) and then reveal the correct answer. I am also able to download the selections the students have made into a spreadsheet to monitor progress throughout the year.
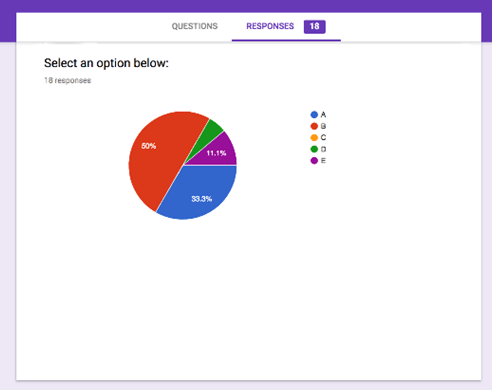
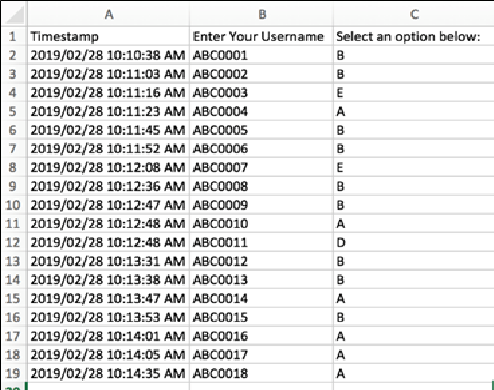
I like using the ‘Exit Ticket’ system. If a student gets an answer wrong, they do not have the anxiety of letting other students know (as in, calling out the wrong answer during class). I also like using the Google Form as it saves paper, all the data is collated in a spreadsheet, and I can keep it all electronically. Completing exit tickets for every lesson means I can monitor how students are progressing as the class proceeds through the course. I then know if they need to slow down, go through concepts in more detail or if they can move swiftly to the next topic. I found students responded better to the exit tickets because they were already in working mode, (after completing the practice problems) and often felt more success, compared to getting a warm up question wrong and then feeling terrible for the remainder of the lesson.
‘Lesson Structure’ and an efficient amount of ‘Explicit Teaching’ are both listed in the Department’s High Impact Teaching Strategies as effective methods to improve outcomes for students. Another of those strategies, ‘Feedback’, is also listed as having perhaps the greatest effect on students’ learning (Hattie, 2009). Timing lessons so that students are practising more than the teacher is talking means there is more of an opportunity for skill improvement with the minimum of ‘waffle’. Giving answers through exit tickets provides immediate, clear and efficient feedback for those students. This is enhanced if the teacher has time to re-teach how to solve a particular question. I have found in my classes that, occasionally, a student will stay in at recess to check how to complete an exit ticket question that they have got wrong to avoid leaving the class without closure.
Why is it important to have regular formative assessment? By placing less emphasis on larger, summative tasks that bring anxiety to students, regular feedback with formative tasks can help students develop a growth mindset that supports the building of skills (McMahon and McDonald, 2016). Formative assessment means that the teacher can provide immediate and useful interventions, rather than marking tests at the end of the topic and thinking ‘Oh well, I have to do this better next year’. I find the exit ticket strategy works for this purpose. I am also using a developmental rubric where student produce ‘I can’ statements, but that is a subject for another article.
Key takeaways for graduate teachers
Graduate teachers should spend their formative years in their career developing a lesson structure that suits them. I believe learning to speak less and to be clear with instruction will help far more than trying to be liked (often a trap amongst new teachers). Alternatively, there is a trap to try to implement every possible fun game or whiz-bang activity they’ve seen somewhere in an ad-hoc fashion to win over student interest. Instead, graduates who work on having an established structure can concentrate most of their energy on building rapport, building enthusiasm for their subject and perfecting classroom management skills. Once the lesson structure is in place, that is the time for graduate teachers to experiment with activities to vary a lesson, then find new and interesting ways to monitor students’ progress.
By routinising a structure that works for you, neither you nor your student has to guess what will happen. They come in, receive information, practice what they have learned and can demonstrate their knowledge. During the time of practice, they can interact, share amongst peers, complete group work, ask you questions or even contribute to discussion. Once you have a structure that works for you, you can start developing the interpersonal skills that make you a memorable, passionate and effective teacher.
Questions to discuss with your mentor
If you can organise your mentor to observe some teaching time in your class you might then discuss some of the following:
- Do I talk too much? Am I too fast in my delivery? Am I too slow?
- How can I explain what I need to do in less time?
- How can I intervene when I notice a pattern of poor performance through formative assessment?
- What mechanisms does the school have in place to support students who are falling behind?
- What are alternative lesson structures that work by other teachers around the school?
References:
Department of Education and Training. 2017, High Impact Teaching Strategies, from https://www.education.vic.gov.au/documents/school/teachers/support/highimpactteachstrat.pdf
Hattie, J. (2009). Visible Learning: A synthesis of over 800 meta-analyses relating to achievement. Milton
McMahon, J and McDonald, S (2016) “Teaching Maths – what does the evidence say actually works?”, The Conversation, https://theconversation.com/teaching-maths-wat-does-the-evidence-say-actually-works-64976 .
Park, UK: Routledge.Lemov, D (2010) Teach like a Champion, John Wiley and Sons Ltd.Sharratt, Lyn.D (2018). Clarity: What Matters in Learning, Teaching and Leading, CORWIN PR INC.
